UNIVERSIDAD BICENTENARIA DE ARAGUA
FACULTAD DE INGENIERÍA
ESCUELA DE INGENIERÍA
NÚCLEO PTO. ORDAZ - EDO. BOLÍVAR
Bachilleres:
Jesús Colmenares
Eddilys Naranjo
Rodrigo Rodríguez
Sergio Ytanare
PRUEBA DE HIPÓTESIS
La
estadística inferencial es el proceso de usar la información de una muestra
para describir el estado de una población. Sin embargo es frecuente que usemos
la información de una muestra para probar un reclamo o conjetura sobre la
población.
Hipótesis
y Niveles de Significancia
En
la prueba de hipótesis se pone a prueba un reclamo hecho sobra la naturaleza de
una población a base de la información de una muestra. El reclamo se llama hipótesis estadística.
Hipótesis
Estadística: Una hipótesis estadística es
un reclamo hecho sobre la naturaleza de una población.
Por ejemplo, la premisa formulada
por un productor de baterías para autos de que su batería dura en promedio 48
meses, es una hipótesis estadística porque el manufacturero no inspecciona la vida
de cada batería que él produce.
Como Establecer la hipótesis Nula y la
Alterna
Hipótesis Nula (H0): premisa, reclamo, o conjetura que se pronuncia sobre la naturaleza de una o varias poblaciones.
Hipótesis Nula (H0): premisa, reclamo, o conjetura que se pronuncia sobre la naturaleza de una o varias poblaciones.
Hipótesis Alterna: Una premisa que es cierta cuando la hipótesis
nula es falsa.
Error
Tipo 1 y Error Tipo 2
A
base de la información de una muestra nosotros podemos cometer dos tipos de
errores en nuestra decisión.
1. Podemos rechazar un H0 que es cierto.
2. Podemos aceptar un H0
que es falso.
El primero se llama error Tipo 1
Error Tipo 1: Cuando rechazamos una Hipótesis Nula
que es cierta cometemos error tipo 1.
Y el segundo error se llama error
Tipo 2.
Error Tipo 2: Cuando aceptamos una Hipótesis Nula que es falsa cometemos error tipo 2.
Nivel
de Significancia (a)
Para ser muy cuidadosos en no cometer el error
tipo 1, debemos especificar la probabilidad de rechazar H0, denotada
por a. A ésta se le llama nivel de
significancia.
Nivel de
Significancia: La probabilidad (a) más alta de rechazar H0
cuando H0 es cierto se llama nivel de significancia.
Comentario: Para mantener la probabilidad de cometer el
error tipo 1 baja, debemos escoger un valor pequeño de a.
Usando
un valor preasignado de a
se construye una región de rechazo o región crítica en la
curva normal estándar o en la curva t que indica si debemos
rechazar H0.
Región Crítica o de
Rechazo: Una región crítica o de rechazo es una parte de
la curva de z o de la curva t donde se rechaza H0.
La
región puede ser de una cola o de dos dependiendo de la hipótesis alterna.
Algunos
ejemplos para el error tipo I serían:
• Se considera que el paciente está enfermo, a pesar de que
en realidad está sano; hipótesis nula: El paciente está sano.
• Se declara culpable al acusado, a pesar de que en realidad
es inocente; hipótesis nula: El acusado es inocente.
• No se permite el ingreso de una persona, a pesar de que
tiene derecho a ingresar; hipótesis nula: La persona tiene derecho a
ingresar.
PASOS
PARA CALCULAR PROBABILIDAD DE ERROR TIPO 2:
1. Establecer la región de
no rechazo para H0 , utilizando la media supuesta en H0 y los datos del problema.
2.
Usar la tabla T-4 para
determinar los puntos críticos correspondientes si la prueba es de dos colas
o la prueba es de cola derecha o si es de cola izquierda.
3. Determinar los valores o
valor de correspondientes a los valores
críticos, utilizando la igualdad
4. Dibujar la distribución
de la media verdadera (correspondiente a Ha verdadera o H0
falsa).
5. Determinar los valores
críticos correspondientes a los valores
de , calculados en el paso 3 utilizando la igualdad
6. Usar la tabla T-4 para determinar el
valor de b.
Potencia
de una prueba estadística
Es la probabilidad de rechazar la hipótesis nula Ho cuando la hipótesis
alternativa es verdadera.
El valor de la
potencia es 1-
b y puede interpretarse como la probabilidad
de rechazar de manera correcta una hipótesis nula falsa.
PASOS PARA ESTABLECER UN ENSAYO DE HIPÓTESIS INDEPENDIENTEMENTE DE LA DISTRIBUCIÓN QUE SE ESTE TRATANDO
- Interpretar correctamente hacia que distribución muestral se ajustan los datos del enunciado.
- Interpretar correctamente los datos del enunciado diferenciando los parámetros de los estadísticos. Así mismo se debe determinar en este punto información implícita como el tipo de muestreo y si la población es finita o infinita.
- Establecer simultáneamente el ensayo de hipótesis y el planteamiento gráfico del problema. El ensayo de hipótesis está en función de parámetros ya que se quiere evaluar el universo de donde proviene la muestra. En este punto se determina el tipo de ensayo (unilateral o bilateral).
- Establecer la regla de decisión. Esta se puede establecer en función del valor crítico, el cual se obtiene dependiendo del valor de (Error tipo I o nivel de significancia) o en función del estadístico límite de la distribución muestral. Cada una de las hipótesis deberá ser argumentada correctamente para tomar la decisión, la cual estará en función de la hipótesis nula o Ho.
- Calcular el estadístico real, y situarlo para tomar la decisión.
- Justificar la toma de decisión y concluir.
ALGUNOS EJEMPLOS...
1) Una empresa está interesada en lanzar un nuevo producto al mercado. Tras realizar una campaña publicitaria, se toma la muestra de 1 000 habitantes, de los cuales, 25 no conocían el producto. A un nivel de significación del 1% ¿apoya el estudio las siguientes hipótesis?
- a. Más del 3% de la población no conoce el nuevo producto.
- b. Menos del 2% de la población no conoce el nuevo producto
Datos:
n = 1000
x = 25
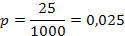
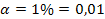
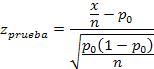
Donde:
x = ocurrencias
n = observaciones
= proporción de la muestra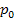
= proporción propuesta
Solución:
a)
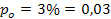
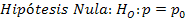
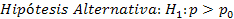
a = 0,01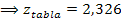 
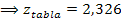
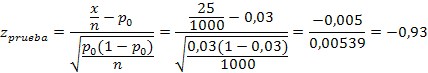
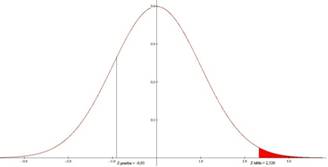
H0 es aceptada, ya que zprueba (-0,93) es menor que ztabla (2,326), por lo que no es cierto que más del 3% de la población no conoce el nuevo producto.
b)
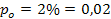
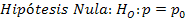
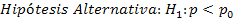
a = 0,01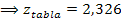
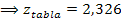
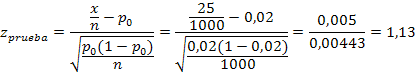
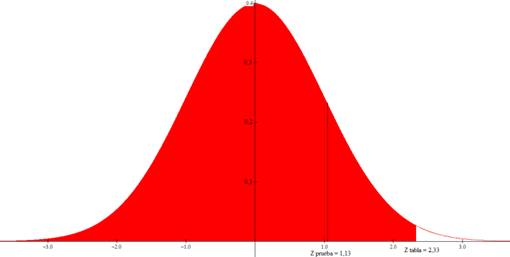
H0 es rechazada, ya que z prueba (1,13) es menor que z tabla (2,326), por lo que es cierto que menos del 2% de la población no conoce el nuevo producto.
2) Cuando las ventas medias, por establecimiento autorizado, de una marca de relojes caen por debajo de las 170,000 unidades mensuales, se considera razón suficiente para lanzar una campaña publicitaria que active las ventas de esta marca. Para conocer la evolución de las ventas, el departamento de marketing realiza una encuesta a 51 establecimientos autorizados, seleccionados aleatoriamente, que facilitan la cifra de ventas del último mes en relojes de esta marca. A partir de estas cifras se obtienen los siguientes resultados: media = 169.411,8 unidades., desviación estándar = 32.827,5 unidades. Suponiendo que las ventas mensuales por establecimiento se distribuyen normalmente; con un nivel de significación del 5 % y en vista a la situación reflejada en los datos. ¿Se considerará oportuno lanzar una nueva campaña publicitaria?
Datos:
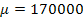
n = 51
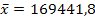
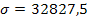
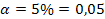
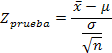
Solución:
H0: ( = 170000
H1: ( < 170000
a = 0,05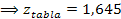 
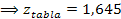
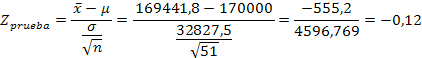
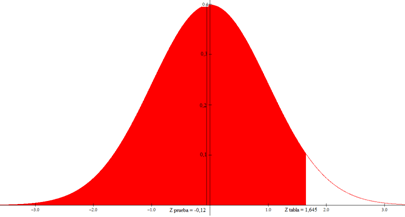
Se rechaza Ho, porque z prueba (-0,12) es menor que z tabla (1,645), por lo tanto se acepta H1: ( < 170000, y se debe considerar oportuno lanzar una nueva campaña publicitaria.
A continuación, un vídeo explicando como confirmamos o negamos una hipótesis... Disfrútenlo!!
Definiendo el error tipo 1 y error tipo 2...
La anterior investigación fue obtenida de las siguientes referencias electrónicas
(links):
http://webdelprofesor.ula.ve/ingenieria/eliana/estad/hipotesis.pdf
http://www.monografias.com/trabajos17/pruebas-de-hipotesis/pruebas-de-hipotesis.shtml
http://www.ditutor.com/inferencia_estadistica/contraste_hip%C3%B3tesis.html
https://www.google.co.ve/url?sa=t&rct=j&q=&esrc=s&source=web&cd=1&cad=rja&ved=0CC4QFjAA&url=http%3A%2F%2Ffacultad.bayamon.inter.edu%2FJMARTINEZ%2Fcursos%2Finge3200%2Fc81.doc&ei=NtD-UOq5Kcmq0AG5_YGoCA&usg=AFQjCNFrOTM_cnRYc7qrK-FIQ96aVFr-Gg&sig2=IlesJQXK3jkrI2RjwPFXQQ&bvm=bv.41248874,d.dmg
http://tesisdeinvestig.blogspot.com/2011/05/prueba-de-hipotesis.html
http://www.monografias.com/trabajos89/ejercicios-resueltos-prueba-hipotesis/ejercicios-resueltos-prueba-hipotesis.shtml
http://www.monografias.com/trabajos89/ejercicios-resueltos-prueba-hipotesis/ejercicios-resueltos-prueba-hipotesis.shtml
